BBoard Theremin

It's been a while, as I sort of got tied up in other things, but one of the devices that's been sitting on my desk for the last few months is a BBoard.

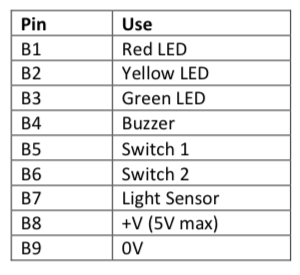
These little boards from Al's Tech Garage have three LED's, two switches, a buzzer and a light sensor, and are designed for plugging into Arduino's. They're pretty nice, though my one gripe would be that the Pins are labeled B1-9, rather than what they actually do, so you'll need to keep this handy table close to hand at all times:

I happen to know Al (of Al's Tech Garage) likes plugging them into Arduino Nano's because they're super cheap. If you're using a Nano, then you can plug them along one side of the board, and use the following Sniff declarations to set up the pins:

make pwr digital output D2

make button2 digital input D4

make button1 digital input D5

make buzzer digital output D6

make greenLight digital output D7

make amberLight digital output D8

make redLight digital output D9

when start

.set pwr to on

This is a little naughty as it uses D2 as the power supply, but the board draws sufficiently small amounts of power that it should be fine.

To plug in to an Uno then you can plug the board in with B1 into A5. You'll find that B7 (the light sensor) falls in the gap where the Arduino has no pins, but then B8 and B9 conveniently land in Vin and 0V. Strictly we shouldn't use Vin here, as if you're using a non-standard power supply it could be greater than 5V, but if you're powering over USB this works great. Of course we can't use the light sensor, but that's probably OK if you're getting started.

In fact the most obvious thing you'll want to do is make a traffic light! Yes - you've got three LED's of the right colours, a couple of buttons and a buzzer all ready to go. what else are you going to do? I've already written about implementing traffic lights a long time ago using the PiBrella. To make that work on the BBoard, just change the pin definitions to the above and you're good to go.

The next thing I wanted to build was a Theremin, using the light sensor to detect how far away my hand was. Unofrtunatly to make that work I couldn't use the "easy plug" method above, so had to use jumper cables to wire up the bboard as:

make light analog input A0

make buzzer digital output A1

make switch digital input A2

To make a sound with the buzzer we need to push it in and out (you can also use it with the Sniff music device, which is really cool, but we won't do that now). That's really easy:

make halfCycle number

make buzzerOn boolean

when start

.forever

..set buzzer to buzzerOn

..wait halfCycle microsecs

..set buzzer to off

..wait halfCycle microsecs

If buzzerOn is "off" then this does nothing. If buzzerOn is "on","yes", or "true" then this pushes the buzzer in and out, making a sound. The frequency is controlled by the variable halfCycle.

For a quick test we can just set the halfCycle something reasonable:

when start

.set halfCycle to 500000/440

440Hz is the standard frequency of the note A, which everything else tunes to. If something is oscillating 440 times per second then the duration of each pulse is 1/440. However we want half of that so we have 0.5/440. Finally we want the duration in microseconds, so we get 500000/440.

Once that was working I could rewrite to use the light sensor:

make frequency number

when start

.forever

..set buzzerOn to switch

..#say [light]

..set frequency to (light*220)+220

..set halfCycle to 500000/frequency

..wait 0.02 secs

the reading of the light sensor can be between 0 and 1, so we set the frequency to a value between 220 and 440Hz (one octave). Then calculate the halfFrequency. We do this 50 times a second, as that was sufficient to produce a smoothly changing note.

And that's it a BBoard Theremin! it works pretty well as long as there's plenty of light.

#IBrokeTheCode

We've been keeping a low profile over the summer, and while we were away I saw an activity at Butlin's, which was developed by Bletchley Park. There were three puzzle's, and each puzzle gave a combination which would open one of three safes. One puzzle was a Caesar Cypher, and another one was a sort of word search. The most interesting one was based on binary, and would make a good class exercise for anyone teaching this stuff. I've tried to reproduce it here:

	17	5	13
1				?
2				?
4				?
8				?
16				?
	4	2	1

We start out with a grid, and mark the squares so that the numbers on the left add up to make the number at the top. So 17 is 16+1, so we mark those two squares:

	17	5	13
1	X	X	X	?
2				?
4		X	X	?
8			X	?
16	X			?
	4	2	1

Here's the completed grid. Next we read off the rows, to find what the numbers at the bottom add up to for each row. The first row is 4+2+1 which makes 7.

	17	5	13
1	X	X	X	7
2				0
4		X	X	3
8			X	1
16	X			4
	4	2	1

Once we've done that for all of the rows we get the answer 70314, which would be the combination to the safe.

However that's not really what this post is about. Inside each of the three safe's there's a two digit number, so once you solve all three puzzles you have a 6 digit number, which opens the final safe!

Inside the final safe is a prize card, proving you solved all the puzzles.

However the prize card also has another puzzle on it.

Each of the letters A to F represent a

single digit. But which ones?

These are the rules:

A != B != C != D != E +D

A+B=C and D+E=F

A>B<C>D<E<F

Pretty much immediately I figured writing a Sniff  program to solve it would be the first thing I did when I got home!

A few months ago we wrote a sudoku solver which used backtracking to generate solutions to any puzzle. That would be a good approach to use here, but its a bit overkill - while that style of solution would be much more efficient in terms of computer time, this problem is simple enough that the computer can check every possible solution in seconds. I'm more worried about programmer time. It's also worth noting that while the sudoku solver might be run several times to solve different puzzles, here once the code is working, we're only going to ever run it once, so it really doesn't matter how long it takes - my time is more important than the computer's!

make count number

make word string

make ok boolean

when start

.repeat 1000000 using count

..set word to [ count ]

..broadcast check and wait

..if ok

...say word

The easiest way to solve this is to generate all of the possible values of A-F and see if they're a valid solution. As there are six digits, there are a million combinations, so we just count from one to 1,000,000. Then we turn that number into a string, and run a script to check if the proposed solution is "OK". If it is then we print out the answer we've found.

So far we could be checking for any set of rules, but next we need to fill in the check script to reject any invalid solutions:

when check

.make A number

.make B number

.make C number

.make D number

.make E number

.make F number

.

.set ok to no

.if not length of word = 6

..stop script

.

.set A to value of letter 1 of word

.set B to value of letter 2 of word

.set C to value of letter 3 of word

.set D to value of letter 4 of word

.set E to value of letter 5 of word

.set F to value of letter 6 of word

.

.#More Tests Here

.

.set ok to yes

this is the beginnings of our "check" script. We make 6 variables for the letters A to F, and we set OK to be no. Then we'll add a series of checks. If we make it all the way to the end then we've passed all the tests, and we've found a solution.

So far I've got the first test - if we don't have a 6 digit number to split up, so we bail.  If we do have 6 digits we can set the six variables.

.

.if A=B

..stop script

.if A=C

..stop script

.if A=D

..stop script

.if A=E

..stop script

.if A=F

..stop script

.

.if B=C

..stop script

.if B=D

..stop script

.if B=E

..stop script

.if B=F

..stop script

.

.if C=D

..stop script

.if C=E

..stop script

.if C=F

..stop script

.

.if D=E

..stop script

.if D=F

..stop script

.

.if E=F

..stop script

.

Testing to check that none of the letters are equal is a bit of a pain - we could do something smarter using two nested loops (and would have to if there were more letters involved), but this works for now. Rewriting this to index through the original word with two loop counters is left as a bonus question!

in fact reading the problem again as I write this, I realise its ambiguous. It seems pretty clear that the intention is that no to numbers are the same, but if we read line one, in the same was as we read line 3, then A!=B, but might be allowed to be equal to C (in which case B would be 0).  We've assume that all digits have to be different. Testing the other way is simpler.

The next few rules, while the look more complex are actually easier to implement:

.

.if not A+B=C

..stop script

.if not D+E=F

..stop script

.

Line two says the two additions must be true, so if they're not we bail again.

.

.if A<B

..stop script

.if B>C

..stop script

.if C<D

..stop script

.if D>E

..stop script

.if E>F

..stop script

.

Finally we check that the inequalities hold. We don't have to worry about the digits being equal (cause that's already tested), so we can just stop if A is less than B, or B > C. In fact some of these tests are redundant, as B can't be greater than C, as A+B=C, but there's little to be gained here by not checking again - that way if we do change the rules later on, then this test will still work.

The program generates 49 solutions, the first few of which are:

314257

314268

314279

325167

325178

325189

Once you see a few, its clear that the solution has two parts (which come from the second line). Once you've found a solution to the first 3 digits, there are potentially several solutions to the second three. I won't list all of the answers, as I don't want to give them all away!

Pokemon TCG: Greedy Dice

Pokemon have been quite a thing in the Sniff household for the last year or two (before "Go" and Sun and Moon made them trendy again), but a recent expansion has been into the Trading Card Game. For those who haven't played, its a card game played with Pokemon cards. However while the basic game is reasonably fun, what makes it interesting is that you can choose what cards make up a your deck. When you get ripped off at Asda's for a "booster pack" it provides 10 new cards, which you can use to replace  cards previously in your deck. Generally you can think of it as a giant game of rock paper scissors, where some cards are better than others, but even some of the weaker ones can come into their own under the right circumstances, so picking the right cards to use is critical.

One card such card is called "Greedy Dice". Within the game there is a pile of 6 "prize" cards, dealt randomly from your deck at the start of the game. Each time you knock out an opponent you get a prize card from your own pile, and if you get all 6 you win! The rule for greedy dice is, if its drawn from the prize pile, you toss a coin and if its heads you get to take another prize card! Two for the price of one!

However once you actually think about it, is it really such a great card to have in your deck? You're limited to 60 cards, so if you put a GD card in, you need to take something out, so you need to be pretty sure its worth it.

So lets do the maths... from 60 cards you have a 1 in 10 chance that one of the 6 prize cards is the GD card. So you'll get something good 1 game in 10? Well not so fast... there are six prize cards, but GD is only useful if one of the first 5. Getting to take an extra prize card does'nt' really help if you've already won. Worst, we forgot about the coin toss, so we get a benefit less than 1 game in 20.

OK that's a bit pointless, but what if we go for it! You're allowed to have up to 4 of each card in your deck, so what happens if we put 4 of them in. That's a big chunk of deck space, but hopefully we'll start to get something out of it...

Now the maths gets a bit more complex, so lets write a program:

make cardsInDeck number 60

make cardsInPrizes number 6

make greedy number 4

make cards list of boolean

make prizes list of boolean

So here we've got 60 cards in a deck, 6 of them are placed as prizes, and of the whole deck 4 of them are greedy dice. To represent the deck and the prizes I've made two lists of booleans - we don't actually care what the cards are, so I'm simply going to store yes or no to record if its a GD.

when game

.delete all of cards

.delete all of prizes

.

.repeat cardsInDeck

..add no to cards

.

.repeat greedy

..delete item 1 of cards

..add yes to cards

So here we go setting up a game. We clear out the cards, and the prizes, and then add 60 regular cards to the list. Then we replace 4 of those with greedy dice. Now we're ready to play!

The game starts when we deal our 6 prizes:

.

.repeat cardsInPrizes

..set deal to pick random 1 to length of cards

..add item deal of cards to prizes

..delete item deal of cards

.

Here we pick six random cards from the deck and place them in the prizes. Finally we just need to see you many of the first 5 prizes are GD:

.

.repeat cardsInPrizes-1

..if item 1 of prizes = yes

...if pick random 1 to 2 = 1

....change found by 1

..delete item 1 of prizes

We pick up the first prize card and if its a GD we toss a coin. If its heads then we've found (and successfully used) a Greedy Dice card. If its tails then we actually loose out in the game, as normally we'd get a useful card as a prize - GD is useless except to win a second prize. We keep track of the number of times we benefit.

make games number 1000000

when start

.set found to 0

.repeat games

..broadcast game and wait

.say join  "found "  join [found]  join " in "  join [games ] " games"

.say [found/games]

Now all we need to do is play a million games! A fraction of a second later, we discover we got an extra prize 167360 times in 1 million games. Thats 16.7% or about once every 6 games.

Of course I'm not the first person to figure this out:  Here some one comes up with the number: 15.83% That's a little but lower than our result, but you read closely you'll see that he's calculated the probability that you'll get one or more useful GD in any game, whereas we've counted the number of times GD's help - sometime more than one per game.

To make the two calculations match, we need to change our scoring:

.

.repeat cardsInPrizes-1

..if item 1 of prizes = yes

...if pick random 1 to 2 = 1

....change found by 1

....stop script

..delete item 1 of prizes

Now when we get a good GD card we call it a win for that match, and stop searching. Doing that we get an exact match up.

So not looking good, and about 1 game in 6 to see any benefit. However if you're new to TCG you might want to try the half deck variant - 30 cards and 3 prizes makes the games a little quicker, and its much easier to build a deck from the the cards you happen to have, rather than having to buy extras to make up a sensible 60. If we have 4 GD from 30 we're more likely to pick them for each prize slot (at the cost of taking up a greater proportion of deck space), which should help... except now we only draw 2 useful prize cards instead of 5, bringing the gain down to a useless 13%.

Either way you can probably do something more interesting with those 4 card slots than GD. Maybe in some future expansion they'll add a trainer card which lets you do something more useful with the GD card, but for now its just a dead card!